In November, Nature published the work of scientists from the University of Geneva (UNIGE) and the Canadian McGill University, who decided to replace the usual PIN code system with a more secure one. In the search for ultra-secure authentication, researchers have proposed reconsidering the ownership factor and relying on a zero-knowledge mathematical proof method in conjunction with the special theory of relativity.
We became curious about how this could work, and we looked inside the scientific work - in the hope of discerning the authentication of the future there.
As the situation usually looks like: the user inserts a card into the ATM, folds his hands over the keyboard, enters a secret PIN code and requests the required amount.
The task itself at the abstract level looks like this:
But in practice, trust can be betrayed on both sides:
So, in search of a more reliable system, scientists decided to “throw out all the assumptions” and invent something better than PINs and one-time codes.
As a first step, they turned to zero-knowledge proof, a principle quite popular in the cryptocurrency space.
The principle was invented in the mid-1980s and is now actively used in practice in cryptography. Its use in the authentication process can be compared to a puzzle game.
"We turned to the three-color coloring problem. One version of this problem uses graphs: a set of nodes, some of which are connected by edges, and some of which are not connected," explains Hugo Zbinden, professor at the Department of Applied Physics at UNIGE. Each node in the graph is assigned one of three possible colors – yellow, blue or red.
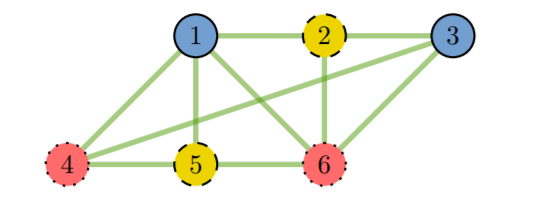
An example graph from the UNIGE study.
In this case, two nodes connected by edges must always be of different colors. So if you make the graph large enough, then choosing a coloring for it can become a serious mathematical problem. Knowing the correct coloring of such a graph will be our proof.
If we transfer this task to ATMs:
The new algorithm from UNIGE has 2 important improvements: the complexity of the algorithm and its carrier. First, even if part of the token responses leaks to attackers, it will be difficult for hackers to recover the full coloring for a large graph. As a basis, the researchers took a three-color vertex coloring of a graph with 5,000 nodes and 10,000 edges. To solve such a problem, enormous computing power is needed. Coloring a graph using a simple enumeration of options is unlikely to be quick. Secondly, we exclude the possibility of hacking on the side of the “verifier”. The ATM itself only has a mechanism for checking control values and does not contain information about coloring the user graph. That is, minus one source of information leakage.
It already sounds convincing. However, this level of system security was not entirely satisfactory for the research team in the long term.
“Encoding functions that are computed in one direction are often difficult to decode, that is, computed in the opposite direction. But this is not impossible,” comments Sébastien Disagnol, a physicist at the University of Geneva and co-author of the study. For example, if you multiply prime numbers and get a very large number, it is difficult to go back to the original numbers. But with the proper persistence and sufficient computing power, it can be done. Targets that are especially attractive to hackers can be subject to debilitating targeted attacks, for which all means are good.
In this regard, scientists put forward a new hypothesis: what about a second device and a second token as an additional authentication factor?
“In this case, the implementation is similar to the police interrogation method. During the investigation, detectives interrogate two suspects at the same time in separate rooms so that they cannot communicate while giving evidence,” says Disagnol. “If the suspects tell the same version of the story, then There's a good chance they're telling the truth."
And this is exactly the moment when Einstein appears on the scene.
In this case, to intercept an account, a hacker will need to hack not one, but two large graphs at the same time. That is, there is a linear complication of the problem. But why, according to scientists, does a solution become impossible?
To make sure that devices cannot communicate with each other, scientists propose relying on the special theory of relativity. The basis of the safety proof is the postulate that we cannot travel faster than the speed of light. This also applies to data transfer speeds.
“With special relativity,” Disagnol continues, “it seems quite reasonable to believe that the safety condition is not a computational constraint, but a physical one... since information cannot travel faster than the speed of light.”
In other words, the researchers are trying to offer hackers a challenge beyond physics. According to the scientists, as long as two ATMs send requests to tokens quickly enough, the delays between the question and the token’s response will always be less than the time for transmitting information over a distance. In a sense, the tokens will not have time to discuss their “alibi” among themselves in order to fake the verification.
In the experiment, scientists tested the operation of such a system at a distance of 390 m and 60 m between ATMs. In the future they plan to reduce the distance to a meter.
Diagram of the organization of the experiment at a distance of 60 m, view of the location from the satellite.
It would seem that the problem is solved. But the researchers have one last question. These relativistic limitations are not so certain when it comes to unconventional physics. And then welcome to quantum computing.
“Suppose I don’t have a graph coloring, but I want to pretend that I do,” Disagnol says of a would-be hacker’s actions. “I could come up with a procedure that uses quantum entanglement between two tokens to answer questions correctly. In some ways I mean, I can cheat."
Scientists are currently speculating whether the security protocol itself could use quantum evidence instead of standard devices.
But for now these are all theories. Even if you don’t go that far, how realistic is it to implement ultra-secure ATMs? Let's look at the practical implementation of the relativistic proof.
To do this, the scientists used field-programmable gate arrays (FPGAs) in their work : a Xilinx SP605 board together with a Spartan-6 XC6SLX45T. Based on them, a token for the user and a reading device for the “ATM” were implemented. At the same time, a separate computer with an Intel core i3 processor and 4 GB of RAM was also installed on the ATM side to monitor and check the consistency of responses.
To synchronize time between the “checkers”, connectivity between ATMs was needed. In the experiment at 390 m, scientists synchronized the “inspectors” using GPS. On 60 m, communication was organized via optics using multi-gigabit transceivers.
Connectivity pattern in two experiments.
Right now, Disagnol says, the main practical problem remains cost of implementation. To create such systems, you need extremely powerful chips, and most likely very expensive ones.
One hypothesis is to use new systems for large companies that own protected information and can afford expensive devices and tokens.
So, perhaps, in the near future, such schemes await us precisely at sites with a high level of security: in banks, data centers, at critical infrastructure facilities.
If you want to dive deeper into the experiment, here are the primary sources of research and interviews with the authors:
We became curious about how this could work, and we looked inside the scientific work - in the hope of discerning the authentication of the future there.
Challenge: ultra-reliable ATM
To illustrate the hypothesis, the scientists took a standard situation where we constantly use PIN codes - withdrawing cash from an ATM.As the situation usually looks like: the user inserts a card into the ATM, folds his hands over the keyboard, enters a secret PIN code and requests the required amount.
The task itself at the abstract level looks like this:
- on the one hand, we have a “prover” - a user who wants to confirm that he is he in order to perform certain actions;
- on the other hand, there is a “verifier” who processes information from the user and verifies it.
But in practice, trust can be betrayed on both sides:
- dishonest "prover" and honest "verifier", for example, when a fraudster has stolen someone else's card and PIN and tries to impersonate someone else to get money;
- an honest “prover” and a dishonest “verifier”, for example, if an ATM is hacked by fraudsters who, when working with an ATM, try to take over the card number and PIN.
So, in search of a more reliable system, scientists decided to “throw out all the assumptions” and invent something better than PINs and one-time codes.
As a first step, they turned to zero-knowledge proof, a principle quite popular in the cryptocurrency space.
How Zero Knowledge Proof Works
“Imagine that I want to demonstrate the proof of a theorem in front of my colleagues,” explains Nicholas Brunner, Professor in the Department of Applied Physics, Faculty of Science at UNIGE. “When I show them the steps of the proof, they will be convinced of its correctness. But at the same time, they will have access to all the information and can easily reproduce the proof." If we don't trust our colleagues and want to prevent the possible recovery of evidence, we need a way to show our knowledge without revealing the information itself. This is essentially a zero-knowledge proof.The principle was invented in the mid-1980s and is now actively used in practice in cryptography. Its use in the authentication process can be compared to a puzzle game.
Geneva and Canadian scientists use a well-known mathematical problem as a “game with cards”.
"We turned to the three-color coloring problem. One version of this problem uses graphs: a set of nodes, some of which are connected by edges, and some of which are not connected," explains Hugo Zbinden, professor at the Department of Applied Physics at UNIGE. Each node in the graph is assigned one of three possible colors – yellow, blue or red.
An example graph from the UNIGE study.
In this case, two nodes connected by edges must always be of different colors. So if you make the graph large enough, then choosing a coloring for it can become a serious mathematical problem. Knowing the correct coloring of such a graph will be our proof.
If we transfer this task to ATMs:
- We provide each user with a token with a unique graph and a pre-programmed solution for three-color coloring. The coloring of the graph regularly changes in accordance with a given algorithm: what was yellow becomes blue, blue becomes red, etc.
- The user connects the device to the external connector of the ATM.
- The ATM checks the token: it sends hundreds of thousands of requests and specifies the color of individual elements of the graph. In practice, experimenters perform this test more than three million times in less than three seconds.
- Since the user has a ready-made solution for coloring on the token, he always quickly and correctly answers queries and confirms his knowledge of the three-color coloring of his graph.
- In this case, during the authentication process, the ATM does not receive a complete coloring of the entire graph, but only makes sure that its coloring is consistent.
The new algorithm from UNIGE has 2 important improvements: the complexity of the algorithm and its carrier. First, even if part of the token responses leaks to attackers, it will be difficult for hackers to recover the full coloring for a large graph. As a basis, the researchers took a three-color vertex coloring of a graph with 5,000 nodes and 10,000 edges. To solve such a problem, enormous computing power is needed. Coloring a graph using a simple enumeration of options is unlikely to be quick. Secondly, we exclude the possibility of hacking on the side of the “verifier”. The ATM itself only has a mechanism for checking control values and does not contain information about coloring the user graph. That is, minus one source of information leakage.
It already sounds convincing. However, this level of system security was not entirely satisfactory for the research team in the long term.
“Encoding functions that are computed in one direction are often difficult to decode, that is, computed in the opposite direction. But this is not impossible,” comments Sébastien Disagnol, a physicist at the University of Geneva and co-author of the study. For example, if you multiply prime numbers and get a very large number, it is difficult to go back to the original numbers. But with the proper persistence and sufficient computing power, it can be done. Targets that are especially attractive to hackers can be subject to debilitating targeted attacks, for which all means are good.
In this regard, scientists put forward a new hypothesis: what about a second device and a second token as an additional authentication factor?
“In this case, the implementation is similar to the police interrogation method. During the investigation, detectives interrogate two suspects at the same time in separate rooms so that they cannot communicate while giving evidence,” says Disagnol. “If the suspects tell the same version of the story, then There's a good chance they're telling the truth."
And this is exactly the moment when Einstein appears on the scene.
What do relativistic principles have to do with it?
So, when using two devices at once, we divide the verification into two prover-verifier pairs. In practice, this means that we connect two separate tokens with unique graphs to two separate ATMs at once. ATMs simultaneously send requests for three-color coloring of graphs.In this case, to intercept an account, a hacker will need to hack not one, but two large graphs at the same time. That is, there is a linear complication of the problem. But why, according to scientists, does a solution become impossible?
To make sure that devices cannot communicate with each other, scientists propose relying on the special theory of relativity. The basis of the safety proof is the postulate that we cannot travel faster than the speed of light. This also applies to data transfer speeds.
“With special relativity,” Disagnol continues, “it seems quite reasonable to believe that the safety condition is not a computational constraint, but a physical one... since information cannot travel faster than the speed of light.”
In other words, the researchers are trying to offer hackers a challenge beyond physics. According to the scientists, as long as two ATMs send requests to tokens quickly enough, the delays between the question and the token’s response will always be less than the time for transmitting information over a distance. In a sense, the tokens will not have time to discuss their “alibi” among themselves in order to fake the verification.
In the experiment, scientists tested the operation of such a system at a distance of 390 m and 60 m between ATMs. In the future they plan to reduce the distance to a meter.
It would seem that the problem is solved. But the researchers have one last question. These relativistic limitations are not so certain when it comes to unconventional physics. And then welcome to quantum computing.
What about "quantum hackers"?
Quantum mechanics allows for a principle called quantum entanglement. Simply put, when two quantum particles, namely particles of light, are entangled, they can interact instantly.“Suppose I don’t have a graph coloring, but I want to pretend that I do,” Disagnol says of a would-be hacker’s actions. “I could come up with a procedure that uses quantum entanglement between two tokens to answer questions correctly. In some ways I mean, I can cheat."
Scientists are currently speculating whether the security protocol itself could use quantum evidence instead of standard devices.
But for now these are all theories. Even if you don’t go that far, how realistic is it to implement ultra-secure ATMs? Let's look at the practical implementation of the relativistic proof.
How relativistic zero-knowledge proof was implemented in practice
During the experiment, it was important for scientists, first of all, to ensure the fastest possible interaction between the “prover” and the “verifier” without delays.To do this, the scientists used field-programmable gate arrays (FPGAs) in their work : a Xilinx SP605 board together with a Spartan-6 XC6SLX45T. Based on them, a token for the user and a reading device for the “ATM” were implemented. At the same time, a separate computer with an Intel core i3 processor and 4 GB of RAM was also installed on the ATM side to monitor and check the consistency of responses.
To synchronize time between the “checkers”, connectivity between ATMs was needed. In the experiment at 390 m, scientists synchronized the “inspectors” using GPS. On 60 m, communication was organized via optics using multi-gigabit transceivers.
Right now, Disagnol says, the main practical problem remains cost of implementation. To create such systems, you need extremely powerful chips, and most likely very expensive ones.
One hypothesis is to use new systems for large companies that own protected information and can afford expensive devices and tokens.
So, perhaps, in the near future, such schemes await us precisely at sites with a high level of security: in banks, data centers, at critical infrastructure facilities.
If you want to dive deeper into the experiment, here are the primary sources of research and interviews with the authors:
