Hacker
Professional
- Messages
- 1,041
- Reaction score
- 847
- Points
- 113
The content of the article
In general, we are convinced that in order to trust a particular security system, you need to understand the technology behind it. So we decided to find a good, relatively accessible guide to ECC - and share it with our readers. It was not possible to find, and we wrote it ourselves - it is in front of you.
I warn you: the topic is complex, you cannot tell about it in a nutshell. There's a lot to discuss here, so make yourself comfortable. But if you need those two words, then here they are: ECC is a new generation of public key cryptosystems that are built on clear mathematical foundations and provide much more serious protection than first generation cryptosystems like RSA. If you want to provide a high level of protection while maintaining performance - it makes sense to turn to ECC. And if you are interested in details, they are below.
Public Key Cryptography: How It All Began
The history of cryptography can be divided into two periods: classical and modern. The watershed here is in 1977, when both the RSA algorithm and the Diffie-Hellman protocol were introduced. A real revolution happened: these were the first cryptographic systems where security was based on number theory. Secure communication became possible without a cipher known to both parties - that is, symmetric -. Prior to that, cryptography had endlessly occupied with the question of how to securely send secret ciphers. Now she could provide evidence-based secure communication between the two parties - without worrying about someone intercepting the key exchange.
Modern cryptography is based on the fact that the key for encrypting data can be public, but the key for decryption is best kept secret. Such systems are called public key cryptographic systems. The first - and still the most common one - is RSA. It is named with the initials of those who first described its algorithm (Ron Rivest, Adi Shamir, Leonard Adleman).
A good public key cryptographic system needs a set of algorithms that are easy to walk in one direction and difficult in the opposite direction. In the case of RSA, the "lightweight" algorithm multiplies two primes. Its "difficult" pair will be factorization - the decomposition of the resulting result into the original factors. Algorithms with this characteristic - "just one way, difficult backward" - are called a trapdoor function (TDF). Finding a good TDF is critical to building a secure public key cryptographic system.
Simply put, the greater the gap between the complexity of passing a function in one direction and in the other, the more reliable the cryptographic system based on it will be.
Miniature RSA Algorithm
RSA is the most popular and best understood of the public key systems. Its safety relies on the fact that multiplication is fast and factoring is slow. Let's take a quick look at how a small RSA system looks and works.
Public key systems usually have two components: a public key and a private key. Encryption works like this: you take a message, apply a mathematical operation to it, and you get a number that looks random. When decrypting, you take this "random" number and apply another operation to get the original message. What is encrypted with the public key can only be decrypted by using the private key.
Computers are not very good at handling arbitrarily large numbers. This problem can be solved by choosing the maximum value and only dealing with numbers that are less than the maximum. It works like a watch with a dial and hands. How to translate them, for example, to 37 hours? Obviously, divide 37 by the maximum - that is, 12 - and tighten up the remainder. So it is here: any calculations that give a result greater than the maximum, we "tighten" to a number in the allowable range.
In RSA, the maximum value (denote it max) is obtained by multiplying two random primes. The public and private keys are two specially selected numbers greater than zero, but less than the maximum value, we denote them by puband priv. To encrypt a number, we multiply it pubonce - and each time we “tighten” it when we exceed the maximum. To decipher the message, we multiply it privonce according to the same rule - and we get the original number. Sounds amazing, but the truth works. When this feature was discovered, it was a big breakthrough.
To create a key pair for RSA, you first take two primes to get the maximum ( max). Then you choose the number for the public key ( pub). As long as you know the two original primes, you can figure out the secret key privfrom the public one. This is how factorization relates to RSA cracking: factoring the maximum value into the original factors allows you to calculate someone's secret key from the public one and decrypt private messages.
Let's consider all this with a specific example. Take the prime numbers 13 and 7, multiply and get the maximum value 91. Take the number 5 as the public key. And then, knowing the initial factors and the maximum, apply the extended Euclidean algorithm and get the secret key - 29.
These parameters ( max = 91, pub = 5, priv = 29) define a fully functional RSA system. We can take a number and multiply it five times to encrypt it, and then take the result, multiply it 29 times, and get the original number.
We use these values to encrypt the CLOUD word.
To represent a message mathematically, you need to turn letters into numbers. The UTF-8 encoding is great for representing the Latin alphabet. Each character has its own number.
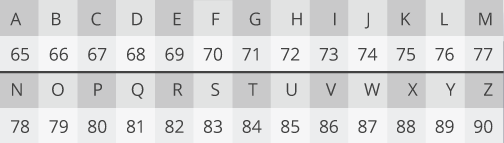
In this encoding, CLOUD looks like 67, 76, 79, 85, 68. All of these numbers are less than our maximum, so we can encrypt them separately.
67 × 67 = 4489 = 30
4489 = 91 × 49 + 30
30 × 67 = 2010 = 8
8 × 67 = 536 = 81
81 × 67 = 5427 = 58
58 and will be the encrypted version 67.
Repeating this process for each of the letters, we get the encrypted CLOUD message in the form
58, 20, 53, 50, 87
To decipher this confusing message, we take each of the resulting numbers - and in the same way we multiply 29 times.
58 × 58 = 3364 = 88 (remember that we "screw up" the number if it exceeds the maximum)
88 × 58 = 5104 = 8
...
9 × 58 = 522 = 67
Voila, we're back to 67. Doing the same with the rest of the numbers, we get the original message.
Conclusion: you can take a number, multiply it some ( pub) times and get a random looking result, and then multiply it another number ( priv) times and return to the original number.
Not such a secret passage
RSA and the Diffie-Hellman protocol were so powerful because they had strong security justifications. Their authors have proven that hacking a system is equal to solving a mathematical problem that is considered difficult to solve. Factorization is a well-known problem and has been studied since antiquity (see the sieve of Eratosthenes). Any breakthrough in this area would be big news and make the inventor rich.
However, factorization is not such a big problem if you solve it step by step. There are special algorithms for factorization - such as the quadratic sieve or the general number field sieve method - and they are moderately successful. Anyway, definitely faster and more economical than the naive approach of guessing pairs of primes.
The efficiency of these algorithms grows as the size of the numbers to be factorized increases all the time. But the gap between the complexity of factorization and multiplication is narrowing - and also due to the growth of numbers (for example, the length of keys). The resources available for decryption are growing - and with them the length of keys grows, and much faster. This is not good for mobile and other low-powered devices with limited computing resources. The gap between expansion and multiplication is not very stable in the long run.
All this means that RSA is far from the ideal system for the cryptography of the future. In an ideal TDF, the round trip operations become more complex at the same rate - in proportion to the growing size of the numbers. We need a more reliable secret passage.
Elliptic Curves: Where to Find a Reliable Back End?
With the advent of RSA and the Diffie-Hellman protocol, an active search began for other mathematically sound cryptography solutions that could serve as a good TDF. And so in 1985, algorithms were proposed based on a mysterious mathematical direction - elliptic curves.
But what exactly is an elliptical curve - and how does the TDF based on it work? Unfortunately, unlike factorization - a thing we inevitably encounter in school - elliptic curves are not familiar to most people. It is not so easy to understand and explain them - however, I will try anyway. (If your eyes have already started to turn glassy, you can skip to the section "What does this all mean?".)
An elliptic curve is a set of points that satisfy a specific mathematical equation. It looks like this:
y² = x³ + ax + b
His graph vaguely resembles the Greek letter Ω (omega) that has fallen to one side.
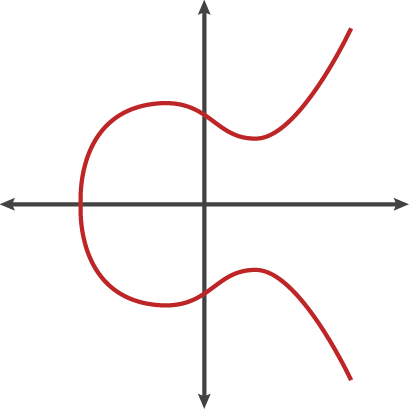
There are other representations of elliptic curves, but technically this is a set of points that satisfy an equation in two variables: one is squared and the other is cubed. However, the elliptical curve is not just a pretty picture: it has a number of features that make it a good foundation for cryptography.
Strange symmetry
Let's take another look at our elliptical curve - and we will find those very features.
One of them is horizontal symmetry. Each point on a curve can be mirrored along an axis x- and you end up on the same curve. Even more interesting is that any non-strictly vertical line intersects the elliptic curve in no more than three places.
Let's imagine that this is such a strange billiards. If you connect two points on a curve, a straight line passing through them will intersect it in exactly one place. Let's put an imaginary billiard ball at a point Aand push it towards the point B. Once it reaches the third and final point on the curve, the ball will bounce either straight up (if it is below the axis x) or straight down (if it is above the axis x) to the other side of the curve.
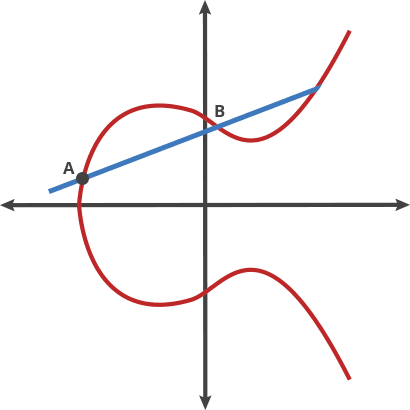
We can connect any two points on the curve and get a new one - for example, connecting Aand B, we got С.
And we can also link these "moves" in order to over and over again connect the original point with the resulting result. So, connecting the point Awith itself, we get the point B; from the starting point Aand the resulting one Bwill come out C; Аand С, in turn, they will give D- and so on.
It turns out that if we have two points - the initial one, "multiplied" by itself n times, and the final one, it is rather difficult to find out what n is equal to. To develop the strange billiards metaphor, imagine a person who plays such a billiards for a while - himself and in a closed room. It will be quite easy for him to push the ball over and over again according to the rules described above. But if someone enters this room and sees where the ball has stopped, then, even knowing the rules of the game and the initial point, he will still not be able to determine the number of hits on the sides - until he repeats all the moves from the starting point to the final one. "Easy there, hard back" - this, as you remember, is the basis for a good TDF.
Curiouser and curiouser
The simplified curve from the previous section looks great and explains the general concept of elliptic curves, but does not show what elliptic curves look like in cryptography.
Here, as in RSA, we have to limit ourselves to numbers in a fixed range. Moreover, we are interested in integers in this range - and the curve does not consist only of them. When solving the equation of the elliptic curve ( y² = x³ + ax + b), we use the same trick with "twisting" the numbers exceeding the maximum. If you take a prime number as the maximum, such an elliptic curve is called simple - and has excellent cryptographic properties.
Here is an example of a curve ( y² = x³ − x + 1) plotted for all values.
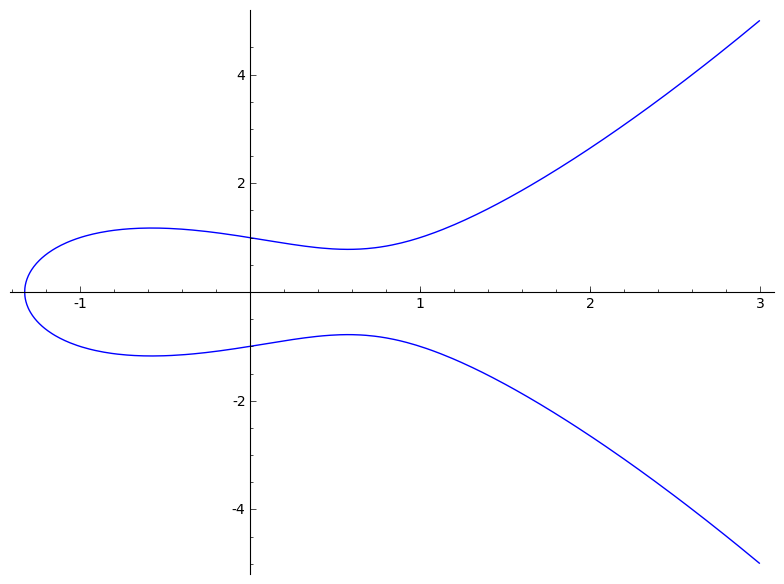
And here is the same curve, but plotted only for integer values with a maximum of 97.
Not at all like a curve in the traditional sense - but this is it. It looks as if the curve, which has suddenly become invisible, has been pinned with buttons at the points where it gives out integer values. And mind you, the horizontal symmetry is preserved.
In fact, we can still play billiards on this curve and connect the dots. And any straight line can still collect no more than three points on itself. Calculating these points is fairly easy. Imagine that the line connecting the two points is a thread that wraps around the curve until it hits the third. It is as if in our strange billiards ball, hitting the side (maximum), magically moved to the opposite side of the table and continued its movement until it hits a point, as in the game "Asteroids".
With this curve representation, it is already possible to encrypt messages. You can imagine the original number of the message as x, get from the equation y- and, accordingly, a point on the curve. In practice, everything is a little more complicated, but the general idea is this.
For a word, FLAREwe get points with coordinates (70.6), (76.48), -, (82.6), (69.22).
(There is no point on this curve at x= 65, but in the real world there are ways to work around this problem.)
The elliptic cryptosystem is defined by: the prime number taken as the maximum, the equation of the curve and the open (starting) point on the curve. The secret key will be a number priv, and the public key will be the starting point connected to itself privonce. The calculation of the secret key from the public key in such a cryptosystem is called the function of the discrete logarithm of the elliptic curve. This seems to be the TDF we were looking for.
What does all this mean?
Calculating the discrete logarithm of an elliptic curve is difficult - which is what elliptic cryptography is based on. Several decades later, mathematicians still have not found an algorithm that would solve this problem better than a simple search. In other words, unlike factorization with its clear mathematical underpinnings, this problem does not seem to have a shortcut that would close the TDF gap. When working with numbers of the same magnitude, solving the discrete logarithm of an elliptic curve is much more difficult than factoring the number. This means that elliptical cryptosystems are stronger than RSA and the Diffie-Hellman protocol.
To illustrate how much stronger, Arjen Lenstra introduced the concept of "Universal Security" (PDF) several years ago. The point is to calculate how much energy is spent cracking a cryptographic algorithm, and compare it with how much water can be boiled with the same energy. A kind of cryptographic carbon footprint. According to his calculations, cracking a 228-bit RSA key requires less energy than boiling one teaspoon of water. By comparison, the energy spent cracking a 228-bit ECC key can boil all the water on the planet. To achieve the same level of security with RSA, you need a 2380-bit key.
With elliptic cryptography, you can use shorter key lengths - and still get the same level of security. And small keys are important, especially in a world where there is more and more cryptography on low-power devices like phones. Multiplying two primes is easier than factoring the result - but when the primes get too long, even multiplication can take a while on low-powered devices. In principle, it is possible to maintain RSA security by increasing the length of the keys, but this will decrease performance on the client. ECC seems to offer a better alternative - high security and short fast keys.
Elliptic curves in action
Elliptical curves were slowly harnessed, but are now rapidly gaining popularity - and spreading very quickly. Elliptic cryptography can now be found in a wide variety of applications: the US government uses it to protect internal communications; the Tor project to provide anonymity; The same mechanism works if you need to verify ownership of bitcoins, send a message to iMessage and encrypt DNS data using DNSCurve; it is also the preferred authentication method for secure surfing over SSL / TLS. Cloudflare uses ECC to provide the perfect Forward Secrecy (PFS) needed to keep your online privacy.
First-generation cryptographic algorithms like RSA and Diffie-Hellman will still work for most applications, but ECC is rapidly gaining popularity as a privacy and security solution on the Internet.
If you open the HTTPS version of the Cloudflare blog through fresh Chrome or Firefox, your browser will use elliptic cryptography. You can verify this yourself - click on the lock to the left of the address bar and select the "Connection" tab.
In this picture, we are primarily interested in the text ECDHE_RSA. ECDHE stands for Elliptic Curve Diffie Hellman Ephemeral is a key exchange mechanism built on elliptic curves. At Cloudflare, it provides perfect forward secrecy on SSL. And with the help of RSA, the server is identified here.
We are using RSA because the Cloudflare SSL certificate is tied to an RSA key pair. But modern browsers also support elliptic curve certificates. If Cloudflare used such a certificate, its designation would look like ECDHE_ECDSA. Server identification would then be done using the Elliptic Curve Digital Signature Algorithm.
The elliptic curve equation for ECDHE that Cloudflare (and Google.com, by the way) uses:
The performance level of ECDSA compared to RSA is impressive. Even with older versions of OpenSSL that are not geared towards elliptic curves, an ECDSA signature with a 256-bit key is more than 20 times faster than an RSA signature with a 2048-bit key.
On a MacBook Pro with OpenSSL 0.9.8, the speed test produces:
Doing 256 bit sign ecdsa's for 10s: 42874 256 bit ECDSA signs in 9.99s
Doing 2048 bit private rsa's for 10s: 1864 2048 bit private RSA's in 9.99s
That is, with ECDSA in the same time, you can get 23 times more signatures than with RSA.
Cloudflare is constantly looking for ways to improve SSL performance. For example, we started using an optimized version of ECC that more than doubles the speed of ECDHE. Elliptical cryptography saves time, power and computing resources - for both the server and the browser - and helps us make the network faster and safer at the same time.
Downside
But not everything is so rosy in the world of elliptical curves - there are also subtle points that prevent them from fully embracing the industry.
One of them is the recently appeared in the news Dual_EC_DRBG (Dual Elliptic Curve Deterministic Random Bit Generator). It is a random number generator standardized by the US National Institute of Standards and Technology (NIST) and promoted by their NSA.
Dual_EC_DRBG generates pseudo-random numbers using the elliptic curve principle. His algorithm takes points on a curve and repeatedly performs the operation to connect these points to get new ones. After its publication, it was reported (PDF) that the generator may have a built-in backdoor - which means that the sequence of the numbers obtained can be fully predicted if there is a correct secret key.
RSA recently recalled several of its products because Dual_EC_DRBG was installed as the default pseudo-random number generator in their security product line. Whether the random number generator was written with a backdoor or not, this does not change the power of the elliptic curve technology itself - but it raises the question of standardization. As we wrote earlier, you need to make sure that your system uses adequately random numbers.
Some skeptical cryptographers generally distrust both NIST itself and its published standards, which the NSA has endorsed. Almost all commonly used elliptic curves fall into this category. Nothing has been heard of attacks on these particular curves - however bad curves exist, and some people think it's better to be careful than to regret.
There is, of course, some progress in the development of curves with efficient arithmetic outside of NIST, including the 25519 curve created by Daniel Bernstein (djb) and the recently computed curves by Paulo Baretto and his comrades - but they are still alive and well before they become widespread. Until these "unconventional" curves are built into browsers, they cannot be used to ensure the security of data transmitted over the network.
Another subtlety of ECC has to do with patents. More than 130 patents covering specific uses of elliptic curves are owned by BlackBerry, after they acquired Certicom in 2009. Many of those patents are licensed for exclusive use by private companies - and even the NSA. Some developers have taken a break because of this - to assess whether their work with ECC violates these patents. In 2007, Certicom filed a lawsuit against Sony - over several uses of elliptic curves - but the lawsuit was dismissed in 2009. There are now a bunch of different implementations of elliptic curve cryptography that are not believed to infringe on these patents - and therefore are widely used.
The ECDSA digital signature has a serious drawback compared to RSA: it requires a good source of entropy. Without sufficient randomness of the numbers, the secret key can be revealed. In 2013, a weak random number generator in Android allowed hackers to find the ECDSA secret key and hack several bitcoin wallets. The Sony PlayStation had a similar vulnerability. Electronic signatures require a good random number generator. Dual_EC_DRBG will certainly not work.
Looking ahead
However, any technology has drawbacks, but the advantages of ECC in comparison with traditional RSA are undeniable - and already widely recognized. Many experts worry that RSA and Diffie-Hellman's mathematical algorithms could be successfully cracked over the coming years - leaving ECC the only reasonable alternative.
- Public Key Cryptography: How It All Began
- Miniature RSA Algorithm
- Not such a secret passage
- Elliptic Curves: Where to Find a Reliable Back End?
- Strange symmetry
- Curiouser and curiouser
- What does all this mean?
- Elliptic curves in action
- Downside
- Looking ahead
In general, we are convinced that in order to trust a particular security system, you need to understand the technology behind it. So we decided to find a good, relatively accessible guide to ECC - and share it with our readers. It was not possible to find, and we wrote it ourselves - it is in front of you.
I warn you: the topic is complex, you cannot tell about it in a nutshell. There's a lot to discuss here, so make yourself comfortable. But if you need those two words, then here they are: ECC is a new generation of public key cryptosystems that are built on clear mathematical foundations and provide much more serious protection than first generation cryptosystems like RSA. If you want to provide a high level of protection while maintaining performance - it makes sense to turn to ECC. And if you are interested in details, they are below.
Public Key Cryptography: How It All Began
The history of cryptography can be divided into two periods: classical and modern. The watershed here is in 1977, when both the RSA algorithm and the Diffie-Hellman protocol were introduced. A real revolution happened: these were the first cryptographic systems where security was based on number theory. Secure communication became possible without a cipher known to both parties - that is, symmetric -. Prior to that, cryptography had endlessly occupied with the question of how to securely send secret ciphers. Now she could provide evidence-based secure communication between the two parties - without worrying about someone intercepting the key exchange.
Modern cryptography is based on the fact that the key for encrypting data can be public, but the key for decryption is best kept secret. Such systems are called public key cryptographic systems. The first - and still the most common one - is RSA. It is named with the initials of those who first described its algorithm (Ron Rivest, Adi Shamir, Leonard Adleman).
A good public key cryptographic system needs a set of algorithms that are easy to walk in one direction and difficult in the opposite direction. In the case of RSA, the "lightweight" algorithm multiplies two primes. Its "difficult" pair will be factorization - the decomposition of the resulting result into the original factors. Algorithms with this characteristic - "just one way, difficult backward" - are called a trapdoor function (TDF). Finding a good TDF is critical to building a secure public key cryptographic system.
Simply put, the greater the gap between the complexity of passing a function in one direction and in the other, the more reliable the cryptographic system based on it will be.
Miniature RSA Algorithm
RSA is the most popular and best understood of the public key systems. Its safety relies on the fact that multiplication is fast and factoring is slow. Let's take a quick look at how a small RSA system looks and works.
Public key systems usually have two components: a public key and a private key. Encryption works like this: you take a message, apply a mathematical operation to it, and you get a number that looks random. When decrypting, you take this "random" number and apply another operation to get the original message. What is encrypted with the public key can only be decrypted by using the private key.
Computers are not very good at handling arbitrarily large numbers. This problem can be solved by choosing the maximum value and only dealing with numbers that are less than the maximum. It works like a watch with a dial and hands. How to translate them, for example, to 37 hours? Obviously, divide 37 by the maximum - that is, 12 - and tighten up the remainder. So it is here: any calculations that give a result greater than the maximum, we "tighten" to a number in the allowable range.
In RSA, the maximum value (denote it max) is obtained by multiplying two random primes. The public and private keys are two specially selected numbers greater than zero, but less than the maximum value, we denote them by puband priv. To encrypt a number, we multiply it pubonce - and each time we “tighten” it when we exceed the maximum. To decipher the message, we multiply it privonce according to the same rule - and we get the original number. Sounds amazing, but the truth works. When this feature was discovered, it was a big breakthrough.
To create a key pair for RSA, you first take two primes to get the maximum ( max). Then you choose the number for the public key ( pub). As long as you know the two original primes, you can figure out the secret key privfrom the public one. This is how factorization relates to RSA cracking: factoring the maximum value into the original factors allows you to calculate someone's secret key from the public one and decrypt private messages.
Let's consider all this with a specific example. Take the prime numbers 13 and 7, multiply and get the maximum value 91. Take the number 5 as the public key. And then, knowing the initial factors and the maximum, apply the extended Euclidean algorithm and get the secret key - 29.
These parameters ( max = 91, pub = 5, priv = 29) define a fully functional RSA system. We can take a number and multiply it five times to encrypt it, and then take the result, multiply it 29 times, and get the original number.
We use these values to encrypt the CLOUD word.
To represent a message mathematically, you need to turn letters into numbers. The UTF-8 encoding is great for representing the Latin alphabet. Each character has its own number.

In this encoding, CLOUD looks like 67, 76, 79, 85, 68. All of these numbers are less than our maximum, so we can encrypt them separately.
67 × 67 = 4489 = 30
4489 = 91 × 49 + 30
30 × 67 = 2010 = 8
8 × 67 = 536 = 81
81 × 67 = 5427 = 58
58 and will be the encrypted version 67.
Repeating this process for each of the letters, we get the encrypted CLOUD message in the form
58, 20, 53, 50, 87
To decipher this confusing message, we take each of the resulting numbers - and in the same way we multiply 29 times.
58 × 58 = 3364 = 88 (remember that we "screw up" the number if it exceeds the maximum)
88 × 58 = 5104 = 8
...
9 × 58 = 522 = 67
Voila, we're back to 67. Doing the same with the rest of the numbers, we get the original message.
Conclusion: you can take a number, multiply it some ( pub) times and get a random looking result, and then multiply it another number ( priv) times and return to the original number.
Not such a secret passage
RSA and the Diffie-Hellman protocol were so powerful because they had strong security justifications. Their authors have proven that hacking a system is equal to solving a mathematical problem that is considered difficult to solve. Factorization is a well-known problem and has been studied since antiquity (see the sieve of Eratosthenes). Any breakthrough in this area would be big news and make the inventor rich.
However, factorization is not such a big problem if you solve it step by step. There are special algorithms for factorization - such as the quadratic sieve or the general number field sieve method - and they are moderately successful. Anyway, definitely faster and more economical than the naive approach of guessing pairs of primes.
The efficiency of these algorithms grows as the size of the numbers to be factorized increases all the time. But the gap between the complexity of factorization and multiplication is narrowing - and also due to the growth of numbers (for example, the length of keys). The resources available for decryption are growing - and with them the length of keys grows, and much faster. This is not good for mobile and other low-powered devices with limited computing resources. The gap between expansion and multiplication is not very stable in the long run.
All this means that RSA is far from the ideal system for the cryptography of the future. In an ideal TDF, the round trip operations become more complex at the same rate - in proportion to the growing size of the numbers. We need a more reliable secret passage.
Elliptic Curves: Where to Find a Reliable Back End?
With the advent of RSA and the Diffie-Hellman protocol, an active search began for other mathematically sound cryptography solutions that could serve as a good TDF. And so in 1985, algorithms were proposed based on a mysterious mathematical direction - elliptic curves.
But what exactly is an elliptical curve - and how does the TDF based on it work? Unfortunately, unlike factorization - a thing we inevitably encounter in school - elliptic curves are not familiar to most people. It is not so easy to understand and explain them - however, I will try anyway. (If your eyes have already started to turn glassy, you can skip to the section "What does this all mean?".)
An elliptic curve is a set of points that satisfy a specific mathematical equation. It looks like this:
y² = x³ + ax + b
His graph vaguely resembles the Greek letter Ω (omega) that has fallen to one side.

There are other representations of elliptic curves, but technically this is a set of points that satisfy an equation in two variables: one is squared and the other is cubed. However, the elliptical curve is not just a pretty picture: it has a number of features that make it a good foundation for cryptography.
Strange symmetry
Let's take another look at our elliptical curve - and we will find those very features.
One of them is horizontal symmetry. Each point on a curve can be mirrored along an axis x- and you end up on the same curve. Even more interesting is that any non-strictly vertical line intersects the elliptic curve in no more than three places.
Let's imagine that this is such a strange billiards. If you connect two points on a curve, a straight line passing through them will intersect it in exactly one place. Let's put an imaginary billiard ball at a point Aand push it towards the point B. Once it reaches the third and final point on the curve, the ball will bounce either straight up (if it is below the axis x) or straight down (if it is above the axis x) to the other side of the curve.

We can connect any two points on the curve and get a new one - for example, connecting Aand B, we got С.
And we can also link these "moves" in order to over and over again connect the original point with the resulting result. So, connecting the point Awith itself, we get the point B; from the starting point Aand the resulting one Bwill come out C; Аand С, in turn, they will give D- and so on.
It turns out that if we have two points - the initial one, "multiplied" by itself n times, and the final one, it is rather difficult to find out what n is equal to. To develop the strange billiards metaphor, imagine a person who plays such a billiards for a while - himself and in a closed room. It will be quite easy for him to push the ball over and over again according to the rules described above. But if someone enters this room and sees where the ball has stopped, then, even knowing the rules of the game and the initial point, he will still not be able to determine the number of hits on the sides - until he repeats all the moves from the starting point to the final one. "Easy there, hard back" - this, as you remember, is the basis for a good TDF.
Curiouser and curiouser
The simplified curve from the previous section looks great and explains the general concept of elliptic curves, but does not show what elliptic curves look like in cryptography.
Here, as in RSA, we have to limit ourselves to numbers in a fixed range. Moreover, we are interested in integers in this range - and the curve does not consist only of them. When solving the equation of the elliptic curve ( y² = x³ + ax + b), we use the same trick with "twisting" the numbers exceeding the maximum. If you take a prime number as the maximum, such an elliptic curve is called simple - and has excellent cryptographic properties.
Here is an example of a curve ( y² = x³ − x + 1) plotted for all values.

And here is the same curve, but plotted only for integer values with a maximum of 97.
Not at all like a curve in the traditional sense - but this is it. It looks as if the curve, which has suddenly become invisible, has been pinned with buttons at the points where it gives out integer values. And mind you, the horizontal symmetry is preserved.
In fact, we can still play billiards on this curve and connect the dots. And any straight line can still collect no more than three points on itself. Calculating these points is fairly easy. Imagine that the line connecting the two points is a thread that wraps around the curve until it hits the third. It is as if in our strange billiards ball, hitting the side (maximum), magically moved to the opposite side of the table and continued its movement until it hits a point, as in the game "Asteroids".
With this curve representation, it is already possible to encrypt messages. You can imagine the original number of the message as x, get from the equation y- and, accordingly, a point on the curve. In practice, everything is a little more complicated, but the general idea is this.
For a word, FLAREwe get points with coordinates (70.6), (76.48), -, (82.6), (69.22).
(There is no point on this curve at x= 65, but in the real world there are ways to work around this problem.)
The elliptic cryptosystem is defined by: the prime number taken as the maximum, the equation of the curve and the open (starting) point on the curve. The secret key will be a number priv, and the public key will be the starting point connected to itself privonce. The calculation of the secret key from the public key in such a cryptosystem is called the function of the discrete logarithm of the elliptic curve. This seems to be the TDF we were looking for.
What does all this mean?
Calculating the discrete logarithm of an elliptic curve is difficult - which is what elliptic cryptography is based on. Several decades later, mathematicians still have not found an algorithm that would solve this problem better than a simple search. In other words, unlike factorization with its clear mathematical underpinnings, this problem does not seem to have a shortcut that would close the TDF gap. When working with numbers of the same magnitude, solving the discrete logarithm of an elliptic curve is much more difficult than factoring the number. This means that elliptical cryptosystems are stronger than RSA and the Diffie-Hellman protocol.
To illustrate how much stronger, Arjen Lenstra introduced the concept of "Universal Security" (PDF) several years ago. The point is to calculate how much energy is spent cracking a cryptographic algorithm, and compare it with how much water can be boiled with the same energy. A kind of cryptographic carbon footprint. According to his calculations, cracking a 228-bit RSA key requires less energy than boiling one teaspoon of water. By comparison, the energy spent cracking a 228-bit ECC key can boil all the water on the planet. To achieve the same level of security with RSA, you need a 2380-bit key.
With elliptic cryptography, you can use shorter key lengths - and still get the same level of security. And small keys are important, especially in a world where there is more and more cryptography on low-power devices like phones. Multiplying two primes is easier than factoring the result - but when the primes get too long, even multiplication can take a while on low-powered devices. In principle, it is possible to maintain RSA security by increasing the length of the keys, but this will decrease performance on the client. ECC seems to offer a better alternative - high security and short fast keys.
Elliptic curves in action
Elliptical curves were slowly harnessed, but are now rapidly gaining popularity - and spreading very quickly. Elliptic cryptography can now be found in a wide variety of applications: the US government uses it to protect internal communications; the Tor project to provide anonymity; The same mechanism works if you need to verify ownership of bitcoins, send a message to iMessage and encrypt DNS data using DNSCurve; it is also the preferred authentication method for secure surfing over SSL / TLS. Cloudflare uses ECC to provide the perfect Forward Secrecy (PFS) needed to keep your online privacy.
First-generation cryptographic algorithms like RSA and Diffie-Hellman will still work for most applications, but ECC is rapidly gaining popularity as a privacy and security solution on the Internet.
If you open the HTTPS version of the Cloudflare blog through fresh Chrome or Firefox, your browser will use elliptic cryptography. You can verify this yourself - click on the lock to the left of the address bar and select the "Connection" tab.
In this picture, we are primarily interested in the text ECDHE_RSA. ECDHE stands for Elliptic Curve Diffie Hellman Ephemeral is a key exchange mechanism built on elliptic curves. At Cloudflare, it provides perfect forward secrecy on SSL. And with the help of RSA, the server is identified here.
We are using RSA because the Cloudflare SSL certificate is tied to an RSA key pair. But modern browsers also support elliptic curve certificates. If Cloudflare used such a certificate, its designation would look like ECDHE_ECDSA. Server identification would then be done using the Elliptic Curve Digital Signature Algorithm.
The elliptic curve equation for ECDHE that Cloudflare (and Google.com, by the way) uses:
Code:
max: 115792089210356248762697446949407573530086143415290314195533631308867097853951
curve: y² = x³ + ax + b
a = 115792089210356248762697446949407573530086143415290314195533631308867097853948
b = 41058363725152142129326129780047268409114441015993725554835256314039467401291The performance level of ECDSA compared to RSA is impressive. Even with older versions of OpenSSL that are not geared towards elliptic curves, an ECDSA signature with a 256-bit key is more than 20 times faster than an RSA signature with a 2048-bit key.
On a MacBook Pro with OpenSSL 0.9.8, the speed test produces:
Doing 256 bit sign ecdsa's for 10s: 42874 256 bit ECDSA signs in 9.99s
Doing 2048 bit private rsa's for 10s: 1864 2048 bit private RSA's in 9.99s
That is, with ECDSA in the same time, you can get 23 times more signatures than with RSA.
Cloudflare is constantly looking for ways to improve SSL performance. For example, we started using an optimized version of ECC that more than doubles the speed of ECDHE. Elliptical cryptography saves time, power and computing resources - for both the server and the browser - and helps us make the network faster and safer at the same time.
Downside
But not everything is so rosy in the world of elliptical curves - there are also subtle points that prevent them from fully embracing the industry.
One of them is the recently appeared in the news Dual_EC_DRBG (Dual Elliptic Curve Deterministic Random Bit Generator). It is a random number generator standardized by the US National Institute of Standards and Technology (NIST) and promoted by their NSA.
Dual_EC_DRBG generates pseudo-random numbers using the elliptic curve principle. His algorithm takes points on a curve and repeatedly performs the operation to connect these points to get new ones. After its publication, it was reported (PDF) that the generator may have a built-in backdoor - which means that the sequence of the numbers obtained can be fully predicted if there is a correct secret key.
RSA recently recalled several of its products because Dual_EC_DRBG was installed as the default pseudo-random number generator in their security product line. Whether the random number generator was written with a backdoor or not, this does not change the power of the elliptic curve technology itself - but it raises the question of standardization. As we wrote earlier, you need to make sure that your system uses adequately random numbers.
Some skeptical cryptographers generally distrust both NIST itself and its published standards, which the NSA has endorsed. Almost all commonly used elliptic curves fall into this category. Nothing has been heard of attacks on these particular curves - however bad curves exist, and some people think it's better to be careful than to regret.
There is, of course, some progress in the development of curves with efficient arithmetic outside of NIST, including the 25519 curve created by Daniel Bernstein (djb) and the recently computed curves by Paulo Baretto and his comrades - but they are still alive and well before they become widespread. Until these "unconventional" curves are built into browsers, they cannot be used to ensure the security of data transmitted over the network.
Another subtlety of ECC has to do with patents. More than 130 patents covering specific uses of elliptic curves are owned by BlackBerry, after they acquired Certicom in 2009. Many of those patents are licensed for exclusive use by private companies - and even the NSA. Some developers have taken a break because of this - to assess whether their work with ECC violates these patents. In 2007, Certicom filed a lawsuit against Sony - over several uses of elliptic curves - but the lawsuit was dismissed in 2009. There are now a bunch of different implementations of elliptic curve cryptography that are not believed to infringe on these patents - and therefore are widely used.
The ECDSA digital signature has a serious drawback compared to RSA: it requires a good source of entropy. Without sufficient randomness of the numbers, the secret key can be revealed. In 2013, a weak random number generator in Android allowed hackers to find the ECDSA secret key and hack several bitcoin wallets. The Sony PlayStation had a similar vulnerability. Electronic signatures require a good random number generator. Dual_EC_DRBG will certainly not work.
Looking ahead
However, any technology has drawbacks, but the advantages of ECC in comparison with traditional RSA are undeniable - and already widely recognized. Many experts worry that RSA and Diffie-Hellman's mathematical algorithms could be successfully cracked over the coming years - leaving ECC the only reasonable alternative.

