Man
Professional
- Messages
- 3,077
- Reaction score
- 614
- Points
- 113
Old Mathematics Breaks Post-Quantum Ciphers
The world of cryptography is gradually preparing for the advent of quantum computing, which uses qubits instead of binary logic. Cryptography is expected to be one of the first applications of quantum computers.
The problem is that modern algorithms like RSA and Diffie-Hellman (including those on elliptic curves) are not able to withstand quantum attacks. Therefore, in July 2022, the US National Institute of Standards and Technology (NIST) published a set of encryption algorithms that are potentially able to withstand hacking on quantum computers - the so-called "post-quantum ciphers".
One of the "post-quantum" ciphers was immediately cracked. But the most interesting thing is the method that the researchers used.
In July 2022, after a multi-stage selection process, NIST identified the optimal general-purpose algorithm CRYSTALS-Kyber and four more general-purpose algorithms BIKE, Classic McEliece, HQC, and SIKE that require improvement.
NIST invited researchers to test the published algorithms for vulnerabilities with a reward of $50,000 for a successful hack.
The SIKE algorithm is based on supersingular isogeny, that is, whirling in a supersingular isogenous graph. SIKE is based on a protocol called SIDH (Supersingular Isogeny Diffie-Hellman).
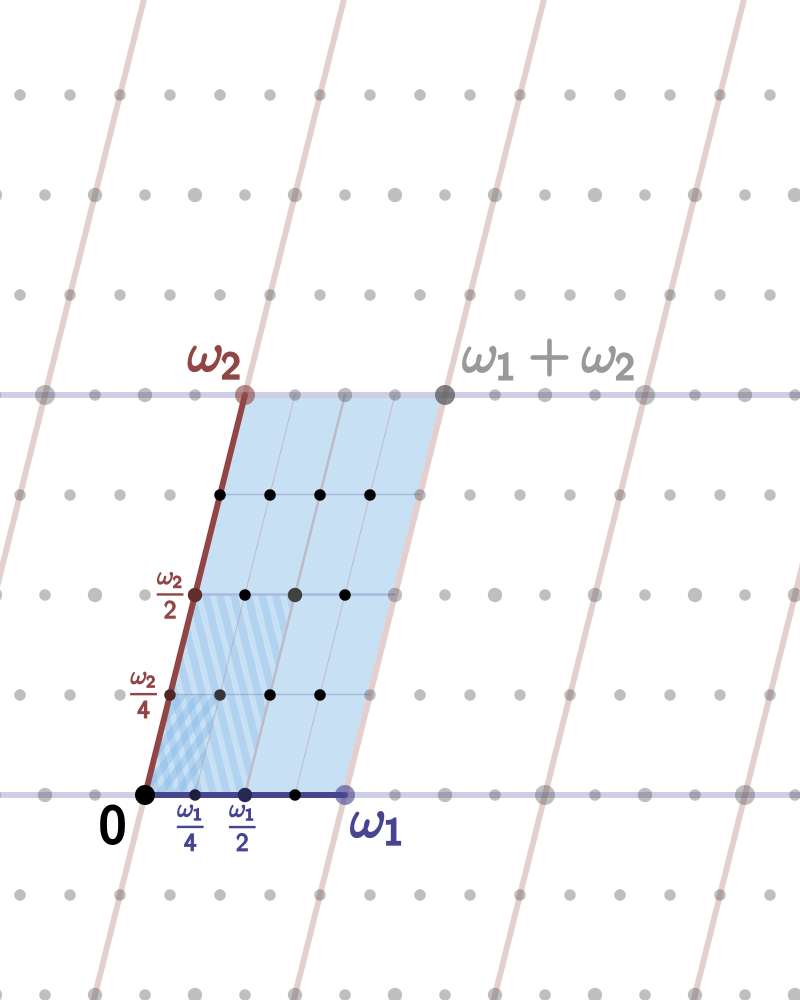
Isogenous elliptic curves to a variety E can be obtained by factoring E by finite subgroups, which are represented as 4-torsion subgroups, source Researchers from the Catholic University of Leuven (Belgium) cracked the SIKE algorithm
quite quickly , for which they received a well-deserved award (this was mentioned on Habr in August 2022). To find the secret key, it was necessary to use only one core of the old Xeon E5-2630v2 processor at a clock frequency of 2.60 GHz. The calculation took less than an hour. But more interesting are the details of this hack, which can be read in a short commentary by mathematics professor Stephen Galbraith, a press release from Queen's University of Canada, and a scientific article by cryptographers Wouter Castryck and Thomas Decru themselves.
The SIKE cipher’s vulnerability turned out to be a mathematical theorem that was probably unfamiliar to the cipher’s authors and the NIST competition’s compilers. It was a 1997 paper by Dr. Ernst Kahni. The theorem has to do with abstractly manipulating mathematical objects to explore their various properties.
Kahni’s theorem discusses the process of “gluing” two elliptic curves together — and under what conditions this procedure can fail. In fact, one of the failure modes described in the paper was used in the SIKE implementation, which provided a natural path to breaking the algorithm using the “adaptive GPST attack” described in the paper “On the Security of Supersingular Isogeny Cryptography” (2016), which built on the aforementioned 1997 paper.
In August 2022, GPST paper co-author Professor Galbraith explained that the key weakness of SIKE is that SIDH does not compute the isogeny directly, but through auxiliary points, where the degree of the isogeny is known. Thus, the attack can be carried out using ready-made mathematical apparatus developed in 1997.
Like GPST, the attack on SIKE simply determines the intermediate curves
 between the base curve
between the base curve
 and the final encryption result
and the final encryption result
 , that is, it ultimately determines the private key.
, that is, it ultimately determines the private key.
“One of the co-authors of the SIKE algorithm expressed surprise that second-order curves can be used to obtain information about elliptic curves. But this was our original strategy in the 1980s and 1990s (and beyond),” Dr. Kahni said in a comment to the university press service.
The successful breaking of SIKE proves that it cannot be a secure means of encryption, narrowing the field of possible candidates for post-quantum encryption technologies. This story once again demonstrates the strength and power of the global scientific community, which acts as a single whole and drives technological progress forward with inevitable consistency.
Kani's 1997 mathematical theorem is a purely theoretical work, and its author hardly foresaw possible practical applications when writing it. There is nothing surprising about this. Even now, scientists in the field of theoretical, fundamental physics and mathematics cannot imagine what real devices their formulas will be used for in 100, 1000 or 10,000 years. For example, the French mathematician Pierre Fermat formulated a curious theorem
in 1637 while factoring large numbers. And only in 1978 was its application found in cryptography. All data encryption methods are mathematics. Therefore, the latest post-quantum encryption systems are also based on the scientific achievements of past centuries.
Source
The world of cryptography is gradually preparing for the advent of quantum computing, which uses qubits instead of binary logic. Cryptography is expected to be one of the first applications of quantum computers.
The problem is that modern algorithms like RSA and Diffie-Hellman (including those on elliptic curves) are not able to withstand quantum attacks. Therefore, in July 2022, the US National Institute of Standards and Technology (NIST) published a set of encryption algorithms that are potentially able to withstand hacking on quantum computers - the so-called "post-quantum ciphers".
One of the "post-quantum" ciphers was immediately cracked. But the most interesting thing is the method that the researchers used.
SIKE algorithm
In July 2022, after a multi-stage selection process, NIST identified the optimal general-purpose algorithm CRYSTALS-Kyber and four more general-purpose algorithms BIKE, Classic McEliece, HQC, and SIKE that require improvement.
NIST invited researchers to test the published algorithms for vulnerabilities with a reward of $50,000 for a successful hack.
The SIKE algorithm is based on supersingular isogeny, that is, whirling in a supersingular isogenous graph. SIKE is based on a protocol called SIDH (Supersingular Isogeny Diffie-Hellman).

Isogenous elliptic curves to a variety E can be obtained by factoring E by finite subgroups, which are represented as 4-torsion subgroups, source Researchers from the Catholic University of Leuven (Belgium) cracked the SIKE algorithm
quite quickly , for which they received a well-deserved award (this was mentioned on Habr in August 2022). To find the secret key, it was necessary to use only one core of the old Xeon E5-2630v2 processor at a clock frequency of 2.60 GHz. The calculation took less than an hour. But more interesting are the details of this hack, which can be read in a short commentary by mathematics professor Stephen Galbraith, a press release from Queen's University of Canada, and a scientific article by cryptographers Wouter Castryck and Thomas Decru themselves.
Theorem of 1997
The SIKE cipher’s vulnerability turned out to be a mathematical theorem that was probably unfamiliar to the cipher’s authors and the NIST competition’s compilers. It was a 1997 paper by Dr. Ernst Kahni. The theorem has to do with abstractly manipulating mathematical objects to explore their various properties.
Kahni’s theorem discusses the process of “gluing” two elliptic curves together — and under what conditions this procedure can fail. In fact, one of the failure modes described in the paper was used in the SIKE implementation, which provided a natural path to breaking the algorithm using the “adaptive GPST attack” described in the paper “On the Security of Supersingular Isogeny Cryptography” (2016), which built on the aforementioned 1997 paper.
In August 2022, GPST paper co-author Professor Galbraith explained that the key weakness of SIKE is that SIDH does not compute the isogeny directly, but through auxiliary points, where the degree of the isogeny is known. Thus, the attack can be carried out using ready-made mathematical apparatus developed in 1997.
Like GPST, the attack on SIKE simply determines the intermediate curves
“One of the co-authors of the SIKE algorithm expressed surprise that second-order curves can be used to obtain information about elliptic curves. But this was our original strategy in the 1980s and 1990s (and beyond),” Dr. Kahni said in a comment to the university press service.
The successful breaking of SIKE proves that it cannot be a secure means of encryption, narrowing the field of possible candidates for post-quantum encryption technologies. This story once again demonstrates the strength and power of the global scientific community, which acts as a single whole and drives technological progress forward with inevitable consistency.
The Importance of Theoretical Science
Kani's 1997 mathematical theorem is a purely theoretical work, and its author hardly foresaw possible practical applications when writing it. There is nothing surprising about this. Even now, scientists in the field of theoretical, fundamental physics and mathematics cannot imagine what real devices their formulas will be used for in 100, 1000 or 10,000 years. For example, the French mathematician Pierre Fermat formulated a curious theorem
in 1637 while factoring large numbers. And only in 1978 was its application found in cryptography. All data encryption methods are mathematics. Therefore, the latest post-quantum encryption systems are also based on the scientific achievements of past centuries.
Source
