This article will cover all the points that anyone who wants to use the shadows and positions of the sun in their investigations needs to know. And here's what we'll be talking about (in case you already know the basics):
Hemispheres, Earth's axes and poles

Sun's altitude and azimuth
How do I describe the position of the Sun in the sky at a certain time? It's simple, you just need to find out how high the Sun is and how far it is from the north direction. It is not difficult to find these values.
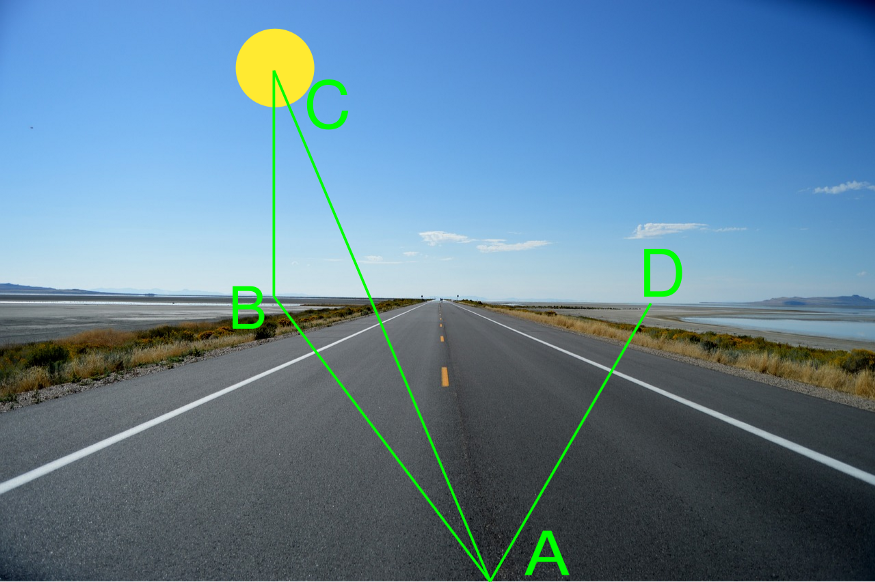
The angle between the lines AB and AC is called the angle of elevation of the Sun. It indicates how high the Sun is.
The angle between AB and AD is called azimuth. It indicates the position of the Sun relative to the north.
Position of the sun and shadow
We all know that the length and direction of shadows change throughout the day (and as the Sun moves across the sky). Shadows are shorter towards noon, when the sun is overhead, and longer in the evening or morning, when the sun is closest to the horizon.
But will the shadow of the same object be the same at the same time in March and September? No.
To understand why this happens, let's look at how the Earth orbits the Sun (during the year).

As you can see, the Earth's orbit is not an even circle, and the Sun is not the center of the orbit, so the distance between the Earth and the Sun changes throughout the year. In June, the sun is closest to the Earth, and in January it is farthest away. And another thing: the angle of the earth's axis is approximately 23.5 degrees.

So when the Sun is closest to the Earth, the sun's rays reach the Earth in this way:
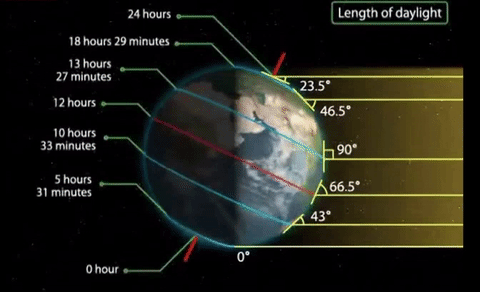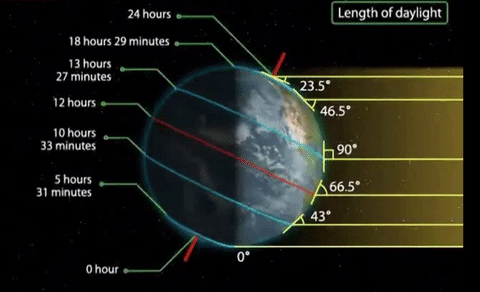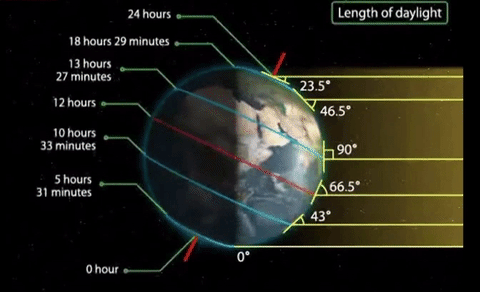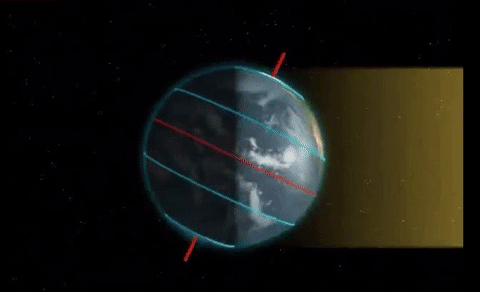
As we can see, the sun's rays hit the Northern Hemisphere in June at a higher angle and for a longer time. Over time, the situation changes to the opposite. And in January, the sun's rays hit the Southern Hemisphere longer and at a higher angle.
Conclusions
From what we've studied above, we can draw two conclusions:
#1. If we know the utol of the Sun's elevation, then we can determine the time.
Why: the height of the Sun affects the length of the shadow, and the length of shadows changes during the day.
#2. If we know the coordinates of the object from which the shadow falls, as well as the azimuth, we can find out the time of year.
Why: The direction and length of the shadow changes at a certain time and at certain times throughout the year. This means that you can simulate the drop of a shadow and choose from all the options that are suitable for our photo.
We use these outputs in OSINT
To use what we've just learned, let's find out when this photo was taken.

First, we'll find out where this photo was taken. We find this place on Google Maps, select objects to confirm the accuracy of the found place. Coordinates: 41.889695, 12.4912546.

The next goal is to find the northern direction of the photo.
This doesn't have an exact methodology, so proceed based on the location of objects in the photo. The technique that is demonstrated in relation to this photo is based on the fact that the position and angle of shooting may distort the angles, but the ratio of the angles to each other will be the same. If the X-angle is twice as large as the Y-angle, then this ratio is constant, regardless of where the photo was taken.
For more information, see the photo above. Do you see a piece of iron with a round base? Let's denote it with the point A.

The left and right columns are denoted by points B and C, respectively. And since the north is always at the top on Google Maps, we draw a straight vertical AD line in the direction of the north.
Then we measure the ratio of the two angles.
DAB angle = 12.01°
Angle BAC = 35.04°
35.04/12.01 = 2.92
The BAC angle is 2.92 times larger than the DAB angle.
In the original photo, select the same lines. Point A is a piece of iron, points B and C are columns.
Draw the AD line so that the DAB angle is 2.92 times smaller than the BAC angle.

Then we'll find the azimuth. In our case, the sun is directly in the south. Therefore, the azimuth is 180 degrees. Remember, the direction of the sun is opposite to the direction of the shadow.

And the last calculation remains, between the length of the object and its shadow.

The shadow is 1.61 times longer than the object. And that's the last piece of information we needed to know.
So, we have
Now we just need to know when the azimuth will be 180°, and the Sun from the north will give the object a shadow 1.61 times longer than the length of the object itself.
To do this, we use a wonderful tool: www.suncalc.org. You can use it to simulate the position of the sun, the length of shadows, and so on.
Enter the location, select the time of year, and then change the time and month until you get the azimuth and shadow length that are identical to your calculations.
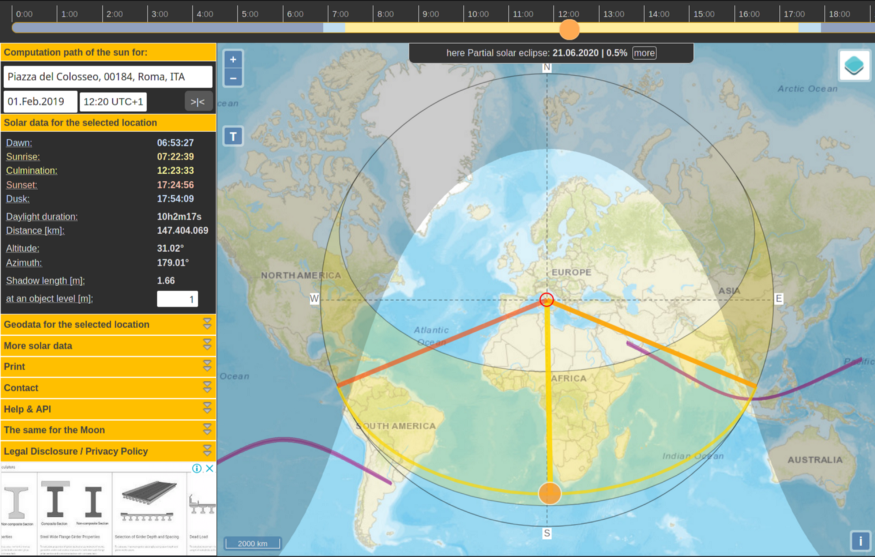
In this case, the best approach is February 1-2, 12.20, when the shadow length was 1.66 and the azimuth was 179.01 (close to 180°).
Another small point - if the shadow falls to the south, then most likely you are in the Southern hemisphere.
- Hemispheres, Earth's axes and poles
- Sun's altitude and azimuth
- Position of the sun and shadow
- Conclusions
- Up-to-date
Hemispheres, Earth's axes and poles

- The Earth has a magnetic field and two poles, North and South (just as magnets have two poles)
- The line that runs from the South Pole to the North Pole is called the axis
- The equator is an abstract line dividing the Earth into two equal parts.
- These two different parts are called the Northern and Southern hemispheres
Sun's altitude and azimuth
How do I describe the position of the Sun in the sky at a certain time? It's simple, you just need to find out how high the Sun is and how far it is from the north direction. It is not difficult to find these values.
- Let's say we are at point A.
- A point on the horizon directly under the Sun is called B.
- The visible center of the Sun is called point C.
- Now draw the AD line (it will point to the North).

The angle between the lines AB and AC is called the angle of elevation of the Sun. It indicates how high the Sun is.
The angle between AB and AD is called azimuth. It indicates the position of the Sun relative to the north.
Position of the sun and shadow
We all know that the length and direction of shadows change throughout the day (and as the Sun moves across the sky). Shadows are shorter towards noon, when the sun is overhead, and longer in the evening or morning, when the sun is closest to the horizon.
But will the shadow of the same object be the same at the same time in March and September? No.
To understand why this happens, let's look at how the Earth orbits the Sun (during the year).

As you can see, the Earth's orbit is not an even circle, and the Sun is not the center of the orbit, so the distance between the Earth and the Sun changes throughout the year. In June, the sun is closest to the Earth, and in January it is farthest away. And another thing: the angle of the earth's axis is approximately 23.5 degrees.

So when the Sun is closest to the Earth, the sun's rays reach the Earth in this way:

As we can see, the sun's rays hit the Northern Hemisphere in June at a higher angle and for a longer time. Over time, the situation changes to the opposite. And in January, the sun's rays hit the Southern Hemisphere longer and at a higher angle.
Conclusions
From what we've studied above, we can draw two conclusions:
#1. If we know the utol of the Sun's elevation, then we can determine the time.
Why: the height of the Sun affects the length of the shadow, and the length of shadows changes during the day.
#2. If we know the coordinates of the object from which the shadow falls, as well as the azimuth, we can find out the time of year.
Why: The direction and length of the shadow changes at a certain time and at certain times throughout the year. This means that you can simulate the drop of a shadow and choose from all the options that are suitable for our photo.
We use these outputs in OSINT
To use what we've just learned, let's find out when this photo was taken.

First, we'll find out where this photo was taken. We find this place on Google Maps, select objects to confirm the accuracy of the found place. Coordinates: 41.889695, 12.4912546.

The next goal is to find the northern direction of the photo.
This doesn't have an exact methodology, so proceed based on the location of objects in the photo. The technique that is demonstrated in relation to this photo is based on the fact that the position and angle of shooting may distort the angles, but the ratio of the angles to each other will be the same. If the X-angle is twice as large as the Y-angle, then this ratio is constant, regardless of where the photo was taken.
For more information, see the photo above. Do you see a piece of iron with a round base? Let's denote it with the point A.

The left and right columns are denoted by points B and C, respectively. And since the north is always at the top on Google Maps, we draw a straight vertical AD line in the direction of the north.
Then we measure the ratio of the two angles.
DAB angle = 12.01°
Angle BAC = 35.04°
35.04/12.01 = 2.92
The BAC angle is 2.92 times larger than the DAB angle.
In the original photo, select the same lines. Point A is a piece of iron, points B and C are columns.
Draw the AD line so that the DAB angle is 2.92 times smaller than the BAC angle.

Then we'll find the azimuth. In our case, the sun is directly in the south. Therefore, the azimuth is 180 degrees. Remember, the direction of the sun is opposite to the direction of the shadow.

And the last calculation remains, between the length of the object and its shadow.

The shadow is 1.61 times longer than the object. And that's the last piece of information we needed to know.
So, we have
- Coordinates: 41.889695, 12.4912546
- Azimuth: 180°
- Shadow length to object length ratio: 1.61
Now we just need to know when the azimuth will be 180°, and the Sun from the north will give the object a shadow 1.61 times longer than the length of the object itself.
To do this, we use a wonderful tool: www.suncalc.org. You can use it to simulate the position of the sun, the length of shadows, and so on.
Enter the location, select the time of year, and then change the time and month until you get the azimuth and shadow length that are identical to your calculations.

In this case, the best approach is February 1-2, 12.20, when the shadow length was 1.66 and the azimuth was 179.01 (close to 180°).
Another small point - if the shadow falls to the south, then most likely you are in the Southern hemisphere.
